How to solve
For Czech version see this blogspot.
1 For example have a following puzzle as 4×4 matrix. Highest number there is 10, so we have to find a path including all numbers from 1 to 10 just once.

2 The end-points in the puzzle are always without duplicities – so we can encircle unique numbers 1 and 10 as a part of the bobble.
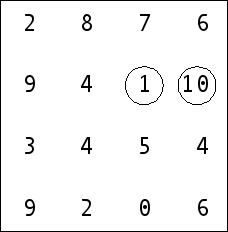
3 Number zero is a fake end-point (number one or ten there) in origin. So zero is a never part of the bobble and we should strike it off.
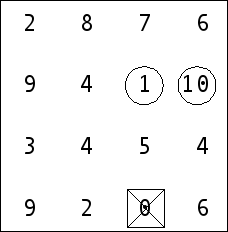
4 Number six in the bottom-right corner becomes an orphan – there is only one valid neighbour (in down from top direction) and thats not enough. The orphan can never be a part of the bobble so we strike it off too.
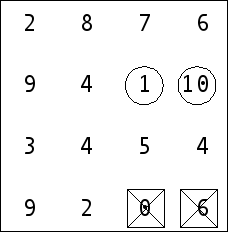
5 Remaining number six in the top-right corner now has to be mandatory. This number has two neighbours only, so they are mandatory too. Number 10 we have already marked, thus we encircle numbers 6 and 7 summarily.
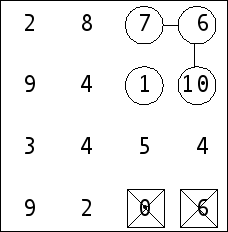
6 Because of number 10 as the end-point now we realize number 4 below 10 as an orphan – so away from here!
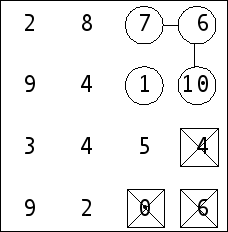
7 Number five is unique across whole puzzle, so it is mandatory. The neighbours in this case are numbers 1 and 4 (on the left) – both have to be the bobble component.
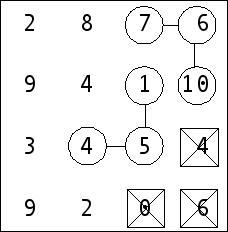
8 The last – not marked yet – number four in the maze cannot be a part of bobble for now, so strike it off.
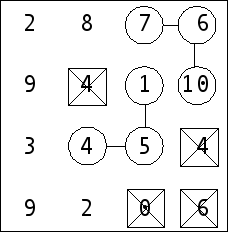
9 At the moment is easy to realize that the rest of the bobble will be around lastly striked number four. Fake numbers 9 and 2 in the last row of matrix we cancel just to be complete.
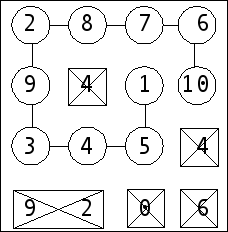
And the puzzle is solved for now!